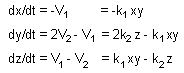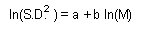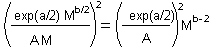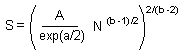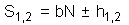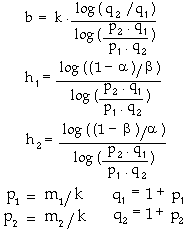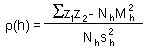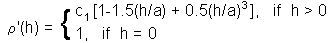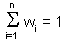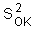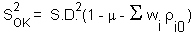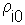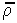| Petri Nets and Estimation of population density and size, geostatistics |
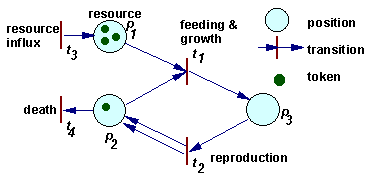
Example of a Petri net |
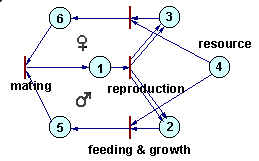
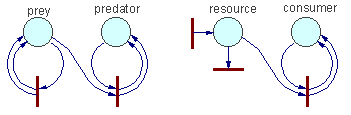
Petri nets can be used to simulate complex ecological interactions within a population and among populations. The figure below is an example of a population with sexual reproduction. More examples can be found in Sharov (1991).Petri net representing a population with sexual reproduction |
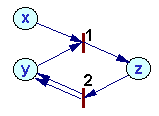
Example1 |
Ex.1 Rates of processes 1 and 2 |
Ex1.Rates of change in token numbers |
Other examples. Coefficient k depends on the rate of organisms'' movement (=temperature). Mass action law assumes that particles move incessantly. However, organisms are not like gas molecules. Predators stop hunting after saturation. A similar saturation effect exists in macromolecules (enzymes). In these cases, mass action law should be replaced by Michaelis-Menton equation: V = kxy/(1+ax). The rest of the algorithm remains the same.Effect of other factors (temperature, age, sex, etc.) can be expressed as variation of coefficient k. As a result, k will become a function of several variables. |
Other examples |
Write differential equations for the following Petri nets assuming that the rate of all processes correspond to the mass action law: |
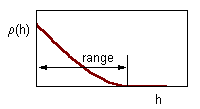
Correlation decreases with distance between samples.The range of correlogram is the lag distance h at which correlation reaches (or becomes close to) zero. Standard statistics can be applied only if inter-sample distance exceeds the range of the correlogram |
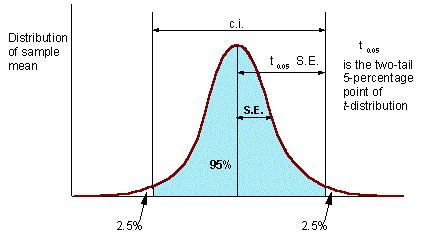
Confidence interval (c.i.) is the interval where the population mean can be found with probability of (1 - P), where P is error probability (e.g., P = 0.05). The number of degrees of freedom d.f. = N - 1 (one d.f. goes for estimation of sample mean). |
Sequential sampling - The first example is the sampling plan targeted at achieving specific accuracy. It is based on the Taylor''s power law |
Coefficients a and b can be estimated using linear regression from several pairs of M and S.D. estimated in different areas with different average population density. Combining two previous equations we get it. |
Mean (M) equals to the total number of recorded individuals (S) in all samples divided by the number of samples (N). Now, we substitute M by S/N, and solve this equation for S |
Stop-lines for accuracy levels of A = 0.1; 0.07; and 0.05. The blue line shows the total number of captured individuals in all samples. Sampling terminates when this line crosses the stop line for selected accuracy level. |
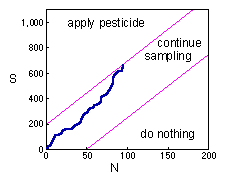
Sequential sampling - The second example is the sequential sampling plan used for decision-making in pest management. This method was developed by Waters (1955; Forest Sci. 1:68-79). It is described in Southwood (1978).Here the blue line again shows the total number of captured individuals in all samples. While the blue line is between magenta inclined lines, sampling continues. If the blue line crosses the upper magenta line, then sampling stops and pesticides are applied against the pest population. If the blue line crosses the lower magenta line, then sampling stops and pesticides are not applied.Deriving the solution of this problem it is too complicated. Thus, we will consider the final result only. |
If the population has a negative binomial distribution (see next lecture), then stop lines correspond to the linear equation |
where |
Next step - Geostatistics: Estimation of Correlogram. Correlogram is a function that shows the correlation among sample points separated by distance h. Correlation usually decreases with distance until it reaches zero. Correlogram is estimated using equation: |
Correlogram is estimated using this equation, where z1 and z2 are organism numbers in two samples separated by lag distance h, summation is performed over all pairs of samples separated by distance h; Nh is the number of pairs of samples separated by distance h; Mh and sh are the mean and the standard deviation of samples separated by distance h (each sample is weighted by the number of pairs of samples in which it is included). |
Estimation of parameters of correlogram model - 1. Exponential model |
Estimation of parameters of correlogram model - 2. Spherical model. where c1 is sill, and a is range. These parameters can be found using the non-linear regression |
Estimation of the surface (=map) using point kriging (ordinary kriging). The value z''o at unsampled location 0 is estimated as a weighted average of sample values z2 at locations i around it |
Weights depend on the degree of correlations among sample points and estimated point. The sum of weights is equal to 1 (this is specific to ordinary kriging): |
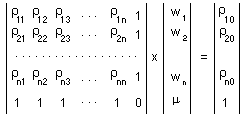
Weights are estimated individually for each point in a regular spatial grid using the system of linear equations, where is the Lagrange parameter; is the correlation between points i and j which is estimated from the variogram model using distance, h, between points i and j; 0 is the estimated point; 1,...,n are sample points. |
Using matrix notation this system can be re-written |
The solution of this matrix equation.Now, weights are found, and thus, it is possible to estimate the value z''o. When these values are estimated for all points in a regular grid, then we get a surface of population density. |
The variance of local estimation |
is equal |
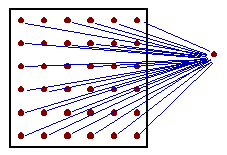
Estimation of the mean value using block kriging. The only difference of block kriging from point kriging is that estimated point (0) is replaced by a block. Consequently, the matrix equation includes "point-to-block" correlations |
Point-to-block correlationis the average correlation between sampled point i and all points within the block (in practice, a regular grid of points within the block is used, as shown in the figure). |
The variance of block estimation |
is equal to it |
is the average correlation within the block (average correlation between all pairs of grid nodes within the block). |
Petri Nets
A formal definition of self reproducing system is proposed using Petri nets. Potential self reproducing system is a subset of places in the Petri net and a subset of internal transitions (a transition is called internal if at least one of starting place and one of final place belong to the subset S) so that the number of tokens in all place in S increases due to firing of internal transitions with specific rates. An actual self-reproducing system is a system that compensates the outflow of its components by reproduction. In a suitable environment eny potential self-reproducing system becomes an actual one. A Petri net can be considered as an "ecosystem" with ecological niches in it.
A more universal factor-process model was developed by Petri (1962). He introduced a class of nets which later were named "Petri nets". These nets have two types of components: positions and transitions (positions = factors, transitions = processes).
The dynamics of a Petri net is a sequence of transition "firing". When a transition is fired then 2 things happen. First, tokens are taken away from positions which have arrows going from these positions to the transition considered. If more than 1 arrow goes from position to transition, then the number of tokens removed from that position is equal to the number of arrows. Second, new tokens are placed on positions indicated by arrows that originate from the transition. The number of tokens placed corresponds again to the number of arrows (in the case of multiple arrows).
For example, in the figure above, when transition t1 is fired, then 1 token is removed from position p1, 1 token is removed from position p2, and 1 token is added on position p3. When transition t2 is fired, then 1 token is removed from position p3, and 1 token is added on position p2. Transition t1 can be interpreted as feeding and growth, and transition t2 as reproduction.
The rate of processes is not defined within a Petri net, it should be specified separately. The rate of chemical reactions is usually defined by mass action law. Mass action law is used in many population ecology models (exponential growth, Lotka-Volterra eqns.). However, there are much more cases in ecology than in chemistry when mass action law does not work. In these cases, the rate of equations is defined in some different way.
How to write differential equations from the Petri net:
1. Write left sides of differential equations for each position i: dxi/dt=
2. For each process (transition) t do the following:
a. Estimate process rate Vt = ktxi xj ... where kt is a constant and xi, xj are the number of tokens in starting positions i, j,... for this process.
b. Subtract Vt from dxi/dt for each starting position i
c. Add Vt to dxi/dt for each ending position i.
See Examples.
Estimation of population density and size
2.1. Censusing a whole population
This method works only if organisms can be easily observed, their numbers are not too big, and the area is well bounded and is not too large. Examples: trees in a small isolated forest; all bird nests are censused in the New-York state (see Pielou 1977).
Migrating populations can be counted using aerial photography. This method is used when the population has seasonal migration. Examples: sandhill cranes and caribou.
2.2. Simple Random or Systematic Sampling
Two possible objectives for sampling:
1. Estimate average population density,
2. Make a map of population density.
Traditionally, random sampling plans were preferred over systematic sampling plans because random sampling helped to avoid subjective selection of sample locations. However, systematic sampling has no elements of subjectivity if sample location is selected prior to examining the area. For example, there is no subjective decisions if we sample every tenth potato plant and count Colorado potato beetles.
Moreover, systematic sampling has an advantage over random sampling if the number of samples is large because of more uniform coverage of the entire sampling area. It is especially important for making population maps. Random sampling can be used if the objective is to estimate the mean population density and the number of samples is not large (<100).
Preferential sampling of specific areas (e.g., high-density areas) was always considered unacceptable. However, modern geostatistical methods and stratified sampling can take advantage of preferential sampling. This shows that the methodology of sampling evolves and old textbooks may give obsolete recipes.
Traditional statistical methods include estimation of the mean population density (M), standard deviation (S.D.), and standard error (S.E.), which is the standard deviation of the sample mean.
The equation for standard error is derived assuming that all samples are independent. This is a very strong assumption which is unrealistic in many situations. Samples separated by small distance are often positively correlated. Before using standard statistics it is important to test if samples are correlated. Spatial correlations are examined using geostatistics. The simplest geostatistical test for spatial autocorrelation is the omnidirectional correlogram:
where z1 and z2 are organism numbers in two samples separated by lag distance h, summation is performed over all pairs of samples separated by distance h; Nh is the number of pairs of samples separated by distance h; Mh and sh are the mean and the standard deviation of samples separated by distance h (each sample is weighted by the number of pairs of samples in which it is included).
Correlation � see pictures.
Precision of sample mean is
A = S.E. / M
There is an empirical rule that precision should be below 0.05 (or 0.1). However, this rule is not universal The only thing that matters in statistics is testing hypotheses. If null-hypothesis is rejected then it does not matter whether A was above or below 0.05. However, in each specific research area, it is useful to find a precision level which is usually sufficient for rejecting null-hypotheses.
Example:. Insect pest population should be suppressed if its density exceeds the economic injury level (EIL). A null-hypothesis is tested that the average density M is equal to EIL. If EIL is within the c.i. for M, then the null-hypothesis cannot be rejected and no decision can be made. In this case, more samples should be taken. If the EIL is outside of the c.i., then null-hypothesis is rejected, and population is suppressed if M > EIL, or not suppressed if M < EIL
2.3. How Many Samples to Take?
There are two major methods for planning the number of samples:
two-step sampling, and
sequential sampling:
Two-step sampling
The number of samples, N, required to achieve specific accuracy level can be estimated from equations for standard error (S.E.) and accuracy, A:
where M is sample mean and S.D. is standard deviation. Here the third equation is derived from the first two equations.
Standard deviation, S.D., is usually not known before sampling. Thus, the first step is to take N1 samples and to estimate N using the equation above. Then, at the second step, take N1 = N - N1 samples.
Taking samples in two steps is possible only if population numbers don''t change between two sampling dates.
Sequential sampling
The main idea of sequential sampling is to take samples until some condition (which is easy to check) is met.
2.4. Elements of geostatistics
Geostatistics is a collection of statistical methods which were traditionally used in geo-sciences. These methods describe spatial autocorrelation among sample data and use it in various types of spatial models. Geostatistical methods were recently adopted in ecology (landscape ecology) and appeared to be very useful in this new area.
Geostatistics changes the entire methodology of sampling. Traditional sampling methods don''t work with autocorrelated data and therefore, the main purpose of sampling plans is to avoid spatial correlations. In geostatistics there is no need in avoiding autocorrelations and sampling becomes less restrictive. Also, geostatistics changes the emphasis from estimation of averages to mapping of spatially-distributed populations.
Spatial autocorrelation can be analyzed using correlograms, covariance functions and variograms (=semivariograms). For simplicity, here we will use correlograms only. Covariance functions and variograms are discussed in the next lecture.
In brief, geostatistical analysis usually has the following steps:
Estimation of correlogram
Estimation of parameters of the correlogram model
Estimation of the surface (=map) using point kriging, or
Estimation of mean values using block kriging
Detailed description of most geostatistical methods can be found in Isaaks and Srivastava (1989). Here we will discuss only the most important elements of geostatistics.
Estimation of Correlogram
Notes:
This is an omnidirectional correlogram; "omnidirectional" means that we don''t care about the direction of lag h.
Serious geostatistical analysis often includes estimation of directional correlograms (see next lecture). It may happen that points are more closely correlated in some direction (e.g., NE-SW) than in other directions. If correlogram depends on direction, then the spatial pattern is called anisotropic. If no anisotropy detected, then it is possible to use the omnidirectional correlogram.
Correlogram equation works only if there are no trends in population density in the study area. If a trend exists, then a non-ergodic correlogram should be used instead (see next lecture).
Estimation of parameters of correlogram model
Estimation of the surface (=map) using point kriging (ordinary kriging)
Estimation of the mean value using block kriging
Advantages of kriging:
It handles spatial autocorrelation
It is not sensitive to preferential sampling in specific areas
It estimates both: local population densities and block averages.
It can replace stratified sampling if the size of aggregations is larger than the inter-sample distance.
References
Isaaks, E. H. and R. M. Srivastava. 1989. An Introduction to Applied Geostatistics. Oxford Univ. Press, New York, Oxford. (a very good introductory textbook)
Deutsch, C. V. and A. G. Journel. 1992. GSLIB. Geostatistical software library and user''s guide. Oxford Univ. Press, Oxford. (software code written in FORTRAN; I have translated a portion of this library into the C-language).
Geostatistics in ecology (review papers):
Rossi, R. E., D. J. Mulla, A. G. Journel and E. H. Franz. 1992. Geostatistical tools for modelling and interpreting ecological spatial dependence. Ecol. Monogr. 62: 277-314.
Liebhold, A. M., R. E. Rossi and W. P. Kemp. 1993. Geostatistics and geographic information systems in applied insect ecology. Annu. Rev. Entomol. 38: 303-327.