| Map projections |
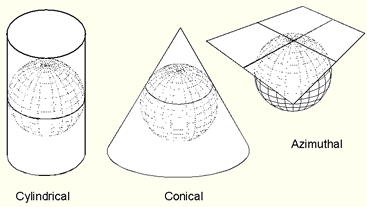
The three classes of map projections |
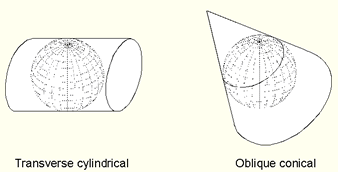
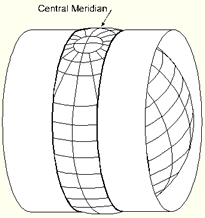
transverse cylindrical and an oblique conical map projection. Both are tangent to the reference surface |
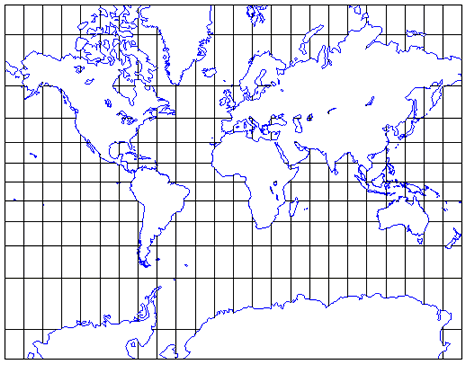
Mercator projection The Mercator projection is a conformal cylindrical projection |
The world mapped in the Transverse Mercator projection (at a small scale) |
Universal Transverse Mercator (UTM) |
Conic projections |
Polyconic projection |
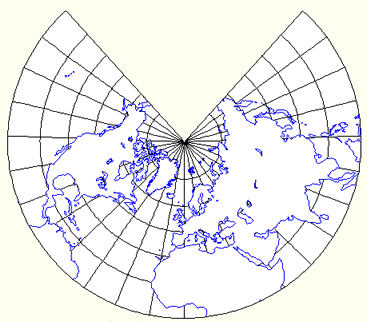
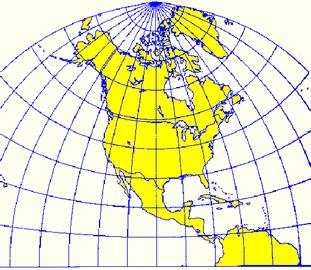
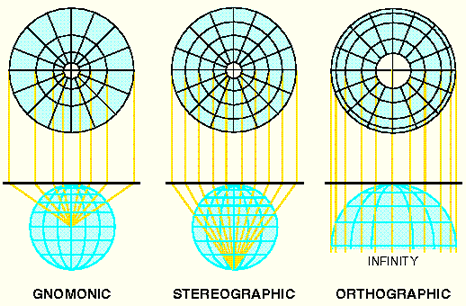
Azimuthal projections |
The transverse (or equatorial) stereographic projection is an example of a conformal azimuthal projection |
Gnomonic projection |
Other map projections: map projection overview - http://www.colorado.edu/geography/gcraft/notes/mapproj/mapproj_f.html |
Central projection on a cylinder
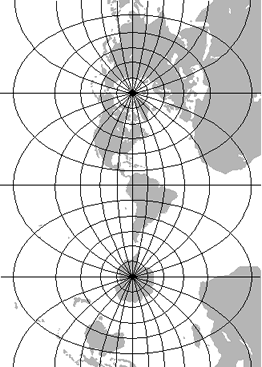
A Lambert equal-area projection
The classification of Map Projections
The Lambert azimuthal equal-area projection is a particular mapping from a sphere to a disk. It accurately represents area in all regions of the sphere, but it does not accurately represent angles. Intuitively, it gives a planar picture of the sphere in which every region appears with the correct area but perhaps a greatly distorted shape. It is named for the Alsatian mathematician Johann Heinrich Lambert, who discovered it in 1772
Mercator projection is a mathematical method of showing a map of the globe on a flat surface. This projection was developed in 1568 by Gerhardus Mercator a Flemish geographer, mathematician, and cartographer. Before this time, navigation charts used by sailors did not correctly account for the recently proven fact that the world was round. Mercator''s equations allowed cartographers (map-makers) to produce charts from which sailors could easily navigate. MercatorÆs projection preserves exactly what sailors needed -- shapes and directions; they were very willing to accept the size distortion.
On a globe, the lines of longitude (measuring east-west position) converge at the poles and the lines of latitudes (measuring north-south position) are equal distance apart. In a Mercator projection, the lines of longitude are straight vertical lines equal distance apart at all latitudes, and horizontal distances are stretched above and below the equator this stretching is exaggerated near the poles. The Mercator projection mathematically stretches vertically distances by the same proportion as the horizontal distances so that shape and direction are preserved. The projection is not useful for latitudes near the poles; J-Track''s projection goes from 78 degrees north latitude to 70 degrees south latitude
Peters projection
German historian and journalist Arno Peters (his Ph.D. dissertation focused on political propaganda) called a press conference in 1973 to announce his "new" map projection that treated each country fairly by representing area accurately. The Peters projection map utilized a rectangular coordinate system that showed parallel lines of latitude and longitude. Skilled at marketing, Arno claimed that his map more fairly displayed third world countries than the "popular" Mercator projection map, which distorts and dramatically enlarges the size of Eurasian and North American countries. The media had a field day with this new map that supposedly made things right for the oppressed people of the world.
Unfortunately, the media fell for Peter''s argument and, due to a lack of understanding about cartography, presented Peters'' idea as the greatest thing since sliced bread. They simultaneously took to vilifying the Mercator projection.
Maps and Charts; What is a Map Projection
Kartografie
Lambert azimuthal equal-area projection
Map projection
Mercator projection