|
|
|
|
|
|
|
|
|
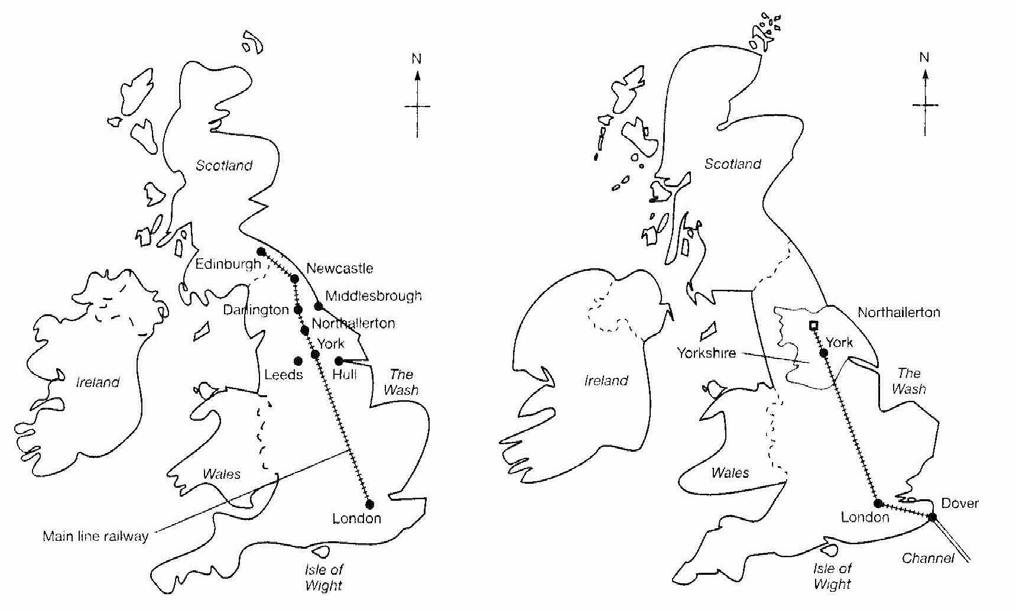
2 mental maps |
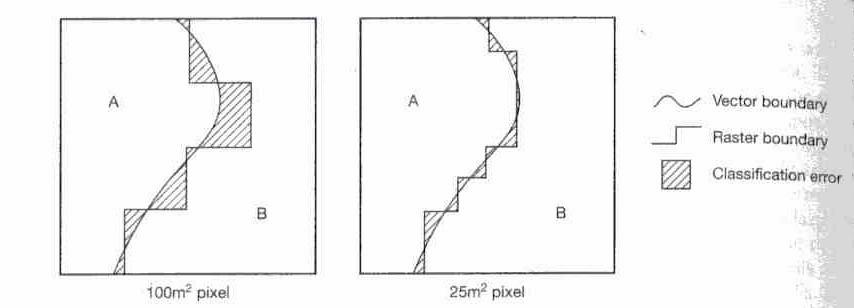
Psychological errors: and line thikeness |
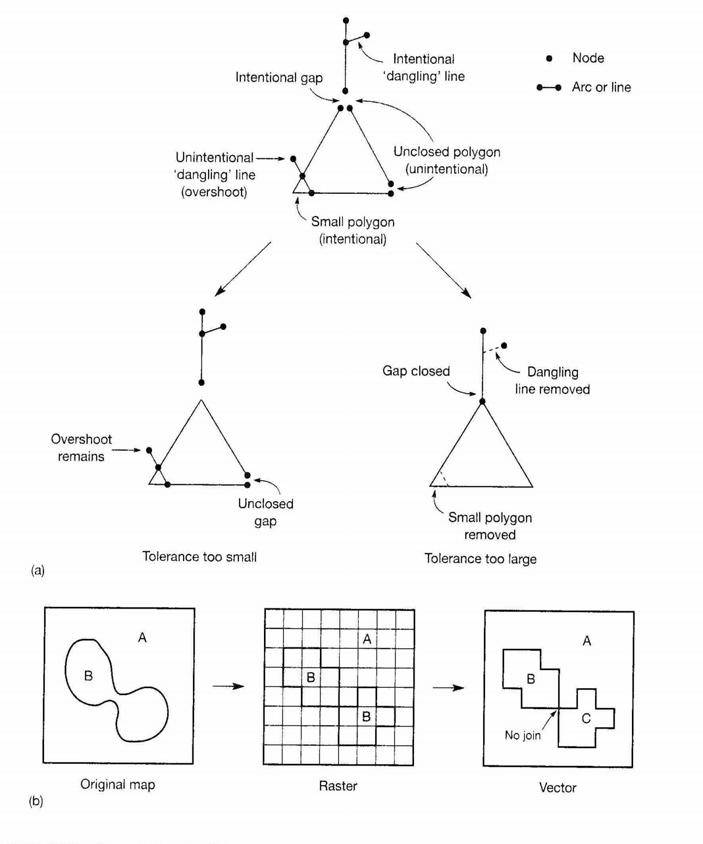
Effects of tolerance on topological cleaning, and topological ambiguities in raster to vector conv. |
|
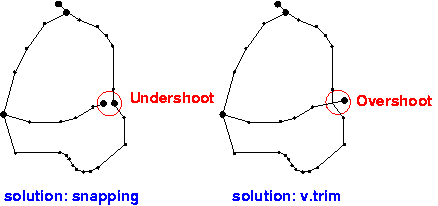
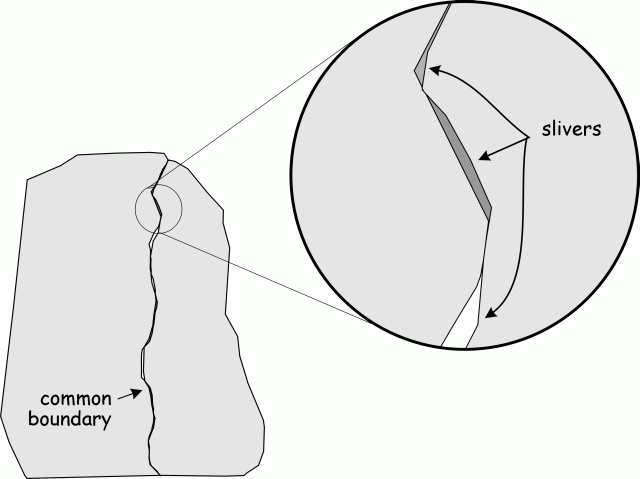
Topological error in vector GIS: |
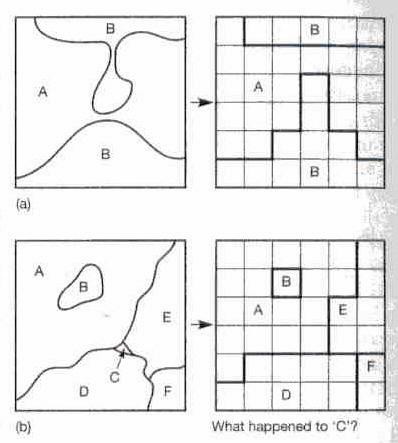
Attribute error result from |
|
|
|
|
|
|
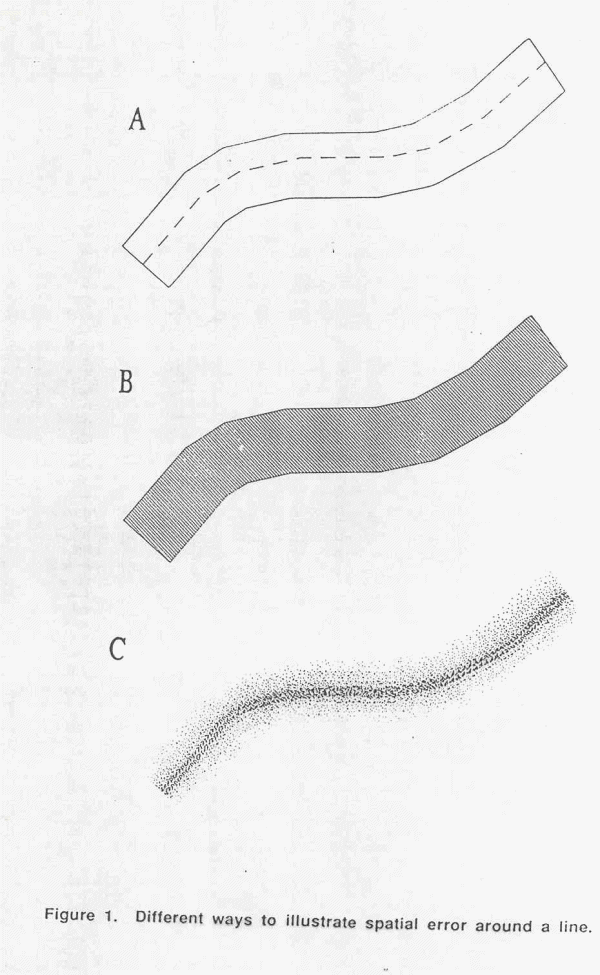
Psychological errors: Difficulties in
perceiving the true centre of the line
being digitized and inability to move
the cursor cross-hairs accurately along
it.
�� Physiological errors: It result from
involuntary muscle spasms that give
rise to random displacement.
�� Line thickness: The thickness of lines
on a map is determined by the
cartographic generation employed.
�� Method of digitizing: Point mode and
stream mode
Effects of tolerance on
topological cleaning
(b) Topological
ambiguities in raster to
vector conversion
Vector to raster
conversion can cause
an interesting
assortment of errors in
the resulting data. For
example
�� Topological errors
�� Loss of small polygons
�� Effects of grid
orientation
�� Variations in grid origin
and datum
GIS operations that can introduce errors include the
classification of data, aggregation or disaggregation
of area data and the integration of data using overlay
technique.
�� Where a certain level of spatial resolution or a certain
set of polygon boundaries are required, data sets
that are not mapped with these may need to be
aggregated or disaggregated to the required level.
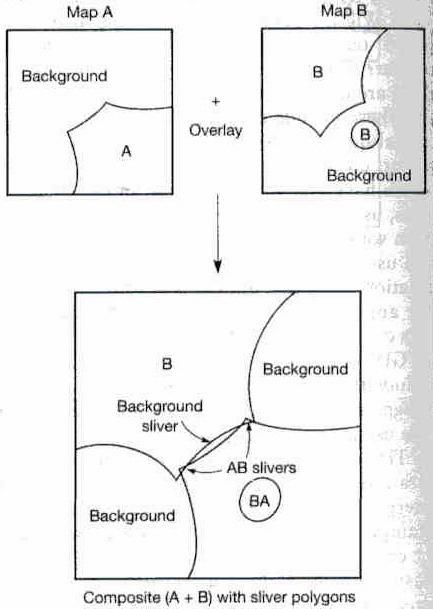
Attribute error result from
positional error (such as
the missing СholeТ feature in
map A that is present as an
island in map B). If one of
the two maps that overlaid
contains an error, then a
classification error will
result in the composite
map (polygon BA).
Measuring error
�� Typos/drawing errors
�� Incorrect implementation error
�� Planning/coordination error
�� Incorrect use of devices error
�� Erroneous methodology error
�� Other human errors
Rounding errors
�� Processing errors
�� Geometric coordinate transformation
�� Map scanning, geometric
approximations
�� Vector to fine raster errors
In numerical modeling and simulation
errors propagate due to the
multiplication of numerical error and
initial measurement error.
�� This presents additional challenges.
Estimating degree of an error is an
interesting area of GIS and
computational science.
Initial data: control quality of measurement,
develop standards, prevent human error.
�� Data models: select correct data models
based on experience or model
appropriateness, reduce errors during
conversion from one to another.
Checking for errors
�� Probably the simplest means of checking for data
errors is by visual inspection.
�� Various statistical methods can be employed to
help pinpoint potential errors.
�� Estimating degree of an error helps in controlling
and correcting errors
Map digitizing Ц errors in digitizing a line or a
geometric shape are estimated by studying the
number of segments for curve approximation and
map properties (distorted, rotated map).
�� PerkalТs concept Ц there is an epsilon error band
around a digitized line within which the data is
considered to be correct.
Statistical approaches for error estimation based on
probabilities of error
�� Estimating the size of the grid and its influence on
data approximation (SwitzerТs method)
�� Double-conversion method for vector to raster
conversion (BregtТs method): convert data twice,
compare differences
Errors associated with overlaying data and other
spatial operations on data arise from inexact
representation of original data and processing errors.
�� Measurement of agreement between an original and
overlaid polygons can be taken (McAlpine and Cook)
Two approaches to the modeling of errors in spatial
data: epsilon modeling and Monte Carlo
simulation.
�� Epsilon modeling is based on a well known
method of line generation (epsilon width).
�� A Monte Carlo simulation approach has also been
used to model the effects of error propagation in
GIS overlays.
Conversion errors Ц develop more reliable algorithms
�� Numerical or progressing errors:
�� maintain consistence of data or result
�� utilize exact computation methods