Lecture2

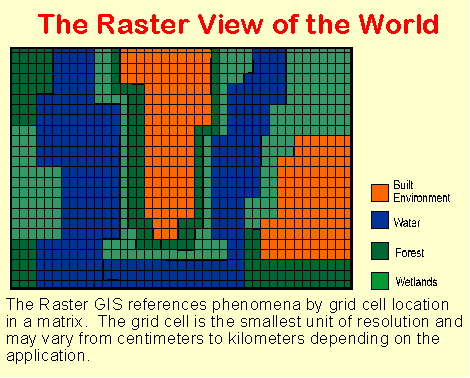
The Raster View of the World
A raster based system displays, locates, and stores graphical data by using a matrix or grid of cells. A unique reference coordinate represents each pixel either at a corner or the centroid. In turn each cell or pixel has discrete attribute data assigned to it. Raster data resolution is dependent on the pixel or grid size and may vary from sub-meter to many kilometers. Because these data are two-dimensional, GISs store various information such as forest cover, soil type, land use, wetland habitat, or other data in different layers. Layers are functionally related map features. Generally, raster data requires less processing than vector data, but it consumes more computer storage space. Scanning remote sensors on satellites store data in raster format. Digital terrain models (DTM) and digital elevation models (DEM) are examples of raster data (Koeln et al 1994 and Huxhold 1991).

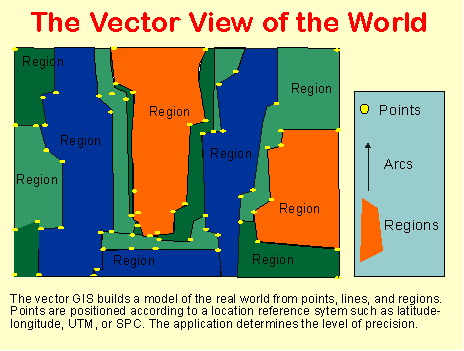
The Vector View of the World
A vector based system displays graphical data as points, lines or curves, or areas with attributes. Cartesian coordinates (i.e., x and y) and computational algorithms of the coordinates define points in a vector system. Lines or arcs are a series of ordered points. Areas or polygons are also stored as ordered lists of points, but by making the beginning and end points the same node the shape is closed and defined. Topological models define the connectivity of vector based systems. Vector systems are capable of very high resolution (less than or equal to .001 inch) and graphical output is similar to hand-drawn maps. This system works well with azimuths, distances, and points, but it requires complex data structures and is less compatible with remote sensing data. Vector data requires less computer storage space and maintaining topological relationships is easier in this system. Digital line graphs (DLG) and TIGER files are examples or vector data (Koeln et al 1994; and Huxhold 1991).

Graphical Comparison of Raster and Vector Systems
It is important to stress that any given real world situation can be represented in both raster and vector modes, the choice is up to the user.
Each of these systems of representation has its advantages and disadvantages:
Method Advantages Disadvantages
Raster Simple data structure
Compatible with remotely sensed or scanned data
Simple spatial analysis procedures
Requires greater storage space on computer
Depending on pixel size, graphical output may be less pleasing
Projection transformations are more difficult
More difficult to represent topological relationships

Vector Requires less disk storage space
Topological relationships are readily maintained
Graphical output more closely resembles hand-drawn maps
More complex data structure
Not as compatible with remotely sensed data
Software and hardware are often more expensive
Some spatial analysis procedures may be more difficult
Overlaying multiple vector maps is often time consuming


It should also be stressed that data modeled in one system can be converted into the other. That is, raster data can be vectorized and vice versa. Many systems even allow data modeled in raster form to be overlaid on vector data and vice versa. In this graphical example, an aerial photo (raster) is overlaid with with supplemental vector information.



--------------------------------------------------------------------------------

3. Organizing Attribute Data
GIS use raster and vector representations to model location, but how they must also record information about the real-world phenomena positioned at each location and the attributes of these phenomena. That is, the GIS must provide a linkage between spatial and non-spatial data. These linkages make the GIS "intelligent" insofar as the user can store and examine information about where things are and what they are like.

The relationship can be diagrammed as a linkage between:

Location <<< >>> What Is There
Spatial Data <<< >>> Non-Spatial Data
Geographic Features <<< >>> Attributes
At the most abstract level, this is a relationship between:

A Locational Symbol <<< >>> Its Meaning
In a raster system, this symbol is a grid cell location in a matrix. In a vector system, the locational symbol may be a one-dimensional point; a two-dimensional line, curve, boundary, or vector; or a three- dimensional area, region, or polygon.
The linkage between symbol and meaning is established by giving every geographic feature at least one unique means of identification, a name or number usually just called its ID. Non-spatial attributes of the feature are then stored, usually in one or more separate files, under this ID number. In other words, locational information is linked to specific information in a database

It is important to realize that this non-spatial data can be filed away in several different forms depending on how it needs to be used and accessed. Perhaps the simplist method is the flat file or spreadsheet, where each geographic feature is matched to one row of data.

3.1 Flat Files and Spreadsheets
A flat file or spreadsheet is a simple method for storing data. All records in this data base have the same number of "fields". Individual records have different data in each field with one field serving as a key to locate a particular record. For example, your social security number may be the key field in a record of your name, address, phone number, sex, ethnicity, place of birth, date of birth, and so on. For an person, or a tract of land there could be hundreds of fields associated with the record. When the number of fields becomes lengthy a flat file is cumbersome to search. Also the key field is usually determined by the programmer and searching by other determinants may be difficult for the user. Although this type of database is simple in its structure, expanding the number of fields usually entails reprogramming. Additionally, adding new records is time consuming, particularly when there are numerous fields. Other methods offer more flexibility and responsiveness in GIS.
3.2 Hierarchical Files
Hierarchical files store data in more than one type of record. This method is usually described as a "parent-child, one-to-many" relationship. One field is key to all records, but data in one record does not have to be repeated in another. This system allows records with similar attributes to be associated together. The records are linked to each other by a key field in a hierarchy of files. Each record, except for the master record, has a higher level record file linked by a key field "pointer". In other words, one record may lead to another and so on in a relatively descending pattern. An advantage is that when the relationship is clearly defined, and queries follow a standard routine, a very efficient data structure results. The database is arranged according to its use and needs. Access to different records is readily available, or easy to deny to a user by not furnishing that particular file of the database. One of the disadvantages is one must access the master record, with the key field determinant, in order to link "downward" to other records.

3.3 Relational Files
Relational files connect different files or tables (relations) without using internal pointers or keys. Instead a common link of data is used to join or associate records. The link is not hierchical. A "matrices of tables" is used to store the information. As long as the tables have a common link they may be combined by the user to form new inquires and data output. This is the most flexible system and is particularly suited to SQL (structured query language). Queries are not limited by a hierarchy of files, but instead are based on relationships from one type of record to another that the user establishes. Because of its flexibility this system is the most popular database model for GIS.

3.4 Flat, Hierarchical, and Relational Files Compared
Structure Advantages Disadvantages
Flat Files Fast data retrieval
Simple structure and easy to program
Difficult to process multiple values of a data item
Adding new data categories requires reprogramming
Slow data retrieval without the key

Hierarchical Files Adding and deleting records is easy
Fast data retrieval through higher level records
Multiple associations with like records in different files
Pointer path restricts access
Each association requires repetitive data in other records
Pointers require large amount of computer storage

Relational Files Easy access and minimal technical training for users
Flexibility for unforeseen inquiries
Easy modification and addition of new relationships, data, and records
Physical storage of data can change without affecting relationships between records
New relations can require considerable processing
Sequential access is slow
Method of storage an disks impacts processing time
Easy to make logical mistakes due to flexibility of relationships between records


Now, let us consider a couple of examples of matching applications to database structures.
Exploratory research--flat files are easy to organize, space is not particular problem
Government agencies--hierarchical systems are particularly attractive
Planning and development--relational might be justified for flexibility


--------------------------------------------------------------------------------

4. Representing Relationships
GIS have the power to record more than location and simple attribute information. In some situations, we will want to examine spatial relationships based upon location, as well as functional and logical relationships among geographic features.
Spatial Relationships

Absolute and relative location
Distance between features
Proximity of features
Features in the "neigborhood" of other features
Direction and movement from place to place
Boolean relationships of "and," "or," "inside," "outside," "intersecting," "non-intersecting," etc.
Functional Relationships among Geographic Features and Their Attributes. This includes information about how features are connected and interact in real-life terms. A road network might be classified functionally from the largest superhighway down to the most isolated rural road or suburban cul-de-sac based upon their role in the overall transportation system. Minor roads and suburban streets "feed" major highways, but are not directly connected to them. As another example in assessing wildlife habitats, various environmental conditions function together to define the optimal living environments for certain species. Within cities, ownership is a functional classification of great importance as is landuse and zoning classification.
Logical Relationships among Geographic Features and Their Attributes. Logical relationships involve "if-then" and "and-or" conditions that must exist among features stored in the dataset. For example, no land may be permitted to be zoned for residential use if it lies within a rivers five-year flood plain. Development may disallowed in the habitat of some endangered species.

Databases can be designed to represent, model, and store information about these relationships as needed for particular applications.



--------------------------------------------------------------------------------

5. The Example of Topological Relationships
Topology is one of the most useful relationships maintained in many spatial databases. It is defined as the mathematics of connectivity or adjacency of points or lines that determines spatial relationships in a GIS. The topological data structure logically determines exactly how and where points and lines connect on a map by means of nodes (topological junctions). The order of connectivity defines the shape of an arc or polygon. The computer stores this information in various tables of the database structure. By storing information in a logical and ordered relationship missing information, e.g., a line segment of a polygon, is readily apparent. A GIS manipulates, analyzes, and uses topological data in determining data relationships.
Network analysis uses topological modeling for determining shortest paths and alternate routes. For example, a GIS for emergency service dispatch may use topological models to quickly ascertain optional routes for emergency vehicles. Automobile commuters perform a similar mental task by altering their route to avoid accidents and traffic congestion. Likewise an electrical utility GIS could rapidly determine different circuit paths to route electricity when service is interrupted by equipment damage. Similarly, political redistricting planners could use certain algorithms to determine logical relationships between population groups and areas for district boundaries.

To see how topology is represented or modeled, it is useful to consider an example to see how connections are coded into a database. This involves recording more than use the absolute location of points, lines, and regions.

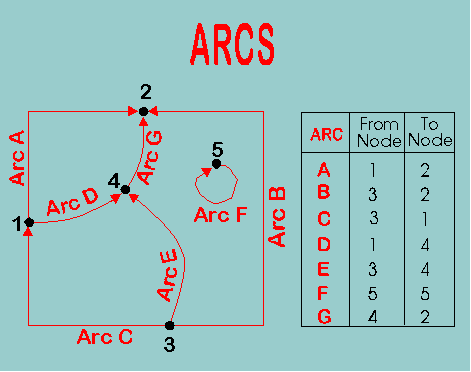
The first step is to record the location of all "nodes," that is endpoints and intersections of lines and boundaries.

Based upon these nodes, "arcs" are defined. These arcs have endpoints, but they are also assigned a direction indicated by the arrowheads. The starting point of the vector is referred to as the "from node" and the destination the "to node." The orientation of a given vector can be assigned in either direction, as long as this direction is recorded and stored in the database

By keeping track of the orientation of arcs, it is possible to use this information to establish routes from node to node or place to place. Thus, if one wants to move from node 3 to node 1, we can locate the necessary connections in the database.

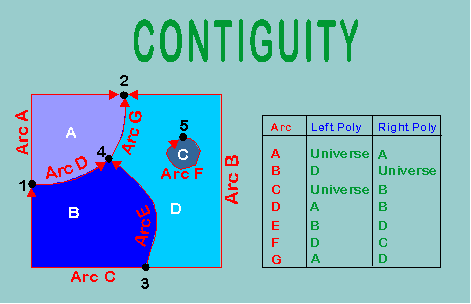
Now, "polygons" are defined by arcs. To define a given polygon, trace around its area in a clockwise direction recording the component arcs and their orientations. If an arc has to be followed in its reverse orientation to make the tracing, it is assigned a negative sign in the database.

Finally, for each arc, one records which polygon lies to the left and right side of its direction of orientation. If an arc is on the edge of the study area, it is bounded by the "universe."

Now that this information has been recorded in the database, it is possible to pose questions about connectivity and location. For example:

What polygons adjoin polygon A? To find the solution, we first look to see what arcs define polygon A, then we check to see what other polygons are defined by these arcs in their n

Lecture 2
Lecture2 part2
Geographer''s Craft
Custom cartography for business
Questions